ニューラルネットワークとは何かご存知でしょうか?最近、機械学習(マシンラーニング)や深層学習(ディープラーニング)という言葉をよく耳にします。一般向けの教材やレクチャーなども開催されていているのですが、言葉だけ聞くととても難しそうで、とっつきにくいイメージがありますよね。
私も人工知能とかそういうものはコンピューターサイエンスのプロのみが理解しうる難しい概念なのだと思っていました。でも、フリーの教材などを使って勉強し始めると、概念だけでも知っておくと非常に面白いものだということがわかってきました。今回は、教養として知りたい方のために、私にでも理解できたニューラルネットワークの概念の基礎知識を共有したいと思います。
ニューラルネットワークとは何か
手書きの数字を判定するネットワーク
私たちがこれからやろうとしているのは、手書きの数字が書かれた画像を与える(入力する・インプットする)と、そこに書かれている数字が0から9のどれかを判定する(出力する・アウトプットする)機械を作ることです。コンピューターの画像はピクセルから成っていますね。それぞれのピクセルに与えられた値を元に、この画像に書かれた手書き数字を値として出力してくれるネットワークを作ろうというわけです。
ニューロン

まず、0から9のいずれかの手書きの数字が書かれた28x28ピクセルの画像があるとします。この画像は黒地に白い文字で数字が書かれた電光掲示板のようなものだと想像してください。黒い部分は電気がついておらず暗い状態、文字の書かれた白い部分は電気がついて明るく点灯しているような状態です。
書かれているのは手書きの文字なので、文字の端っこの部分は筆圧が弱く、白でも黒でもないグレーのエッジがあると思ってください。黒い部分を0、白い部分を1、その間のグレーの部分は明るさによって0から1の間の、0.3や0.7といった小数で表されるものとします。このピクセルのように、値を持つものをニューロンと呼びます。この画像は28x28ピクセルあるので、全部で784ニューロンの入力層(Imput Layer)から成り、それぞれのニューロンには0から1の間の値が当てられているということになります。
隠れ層(Hidden Layers)
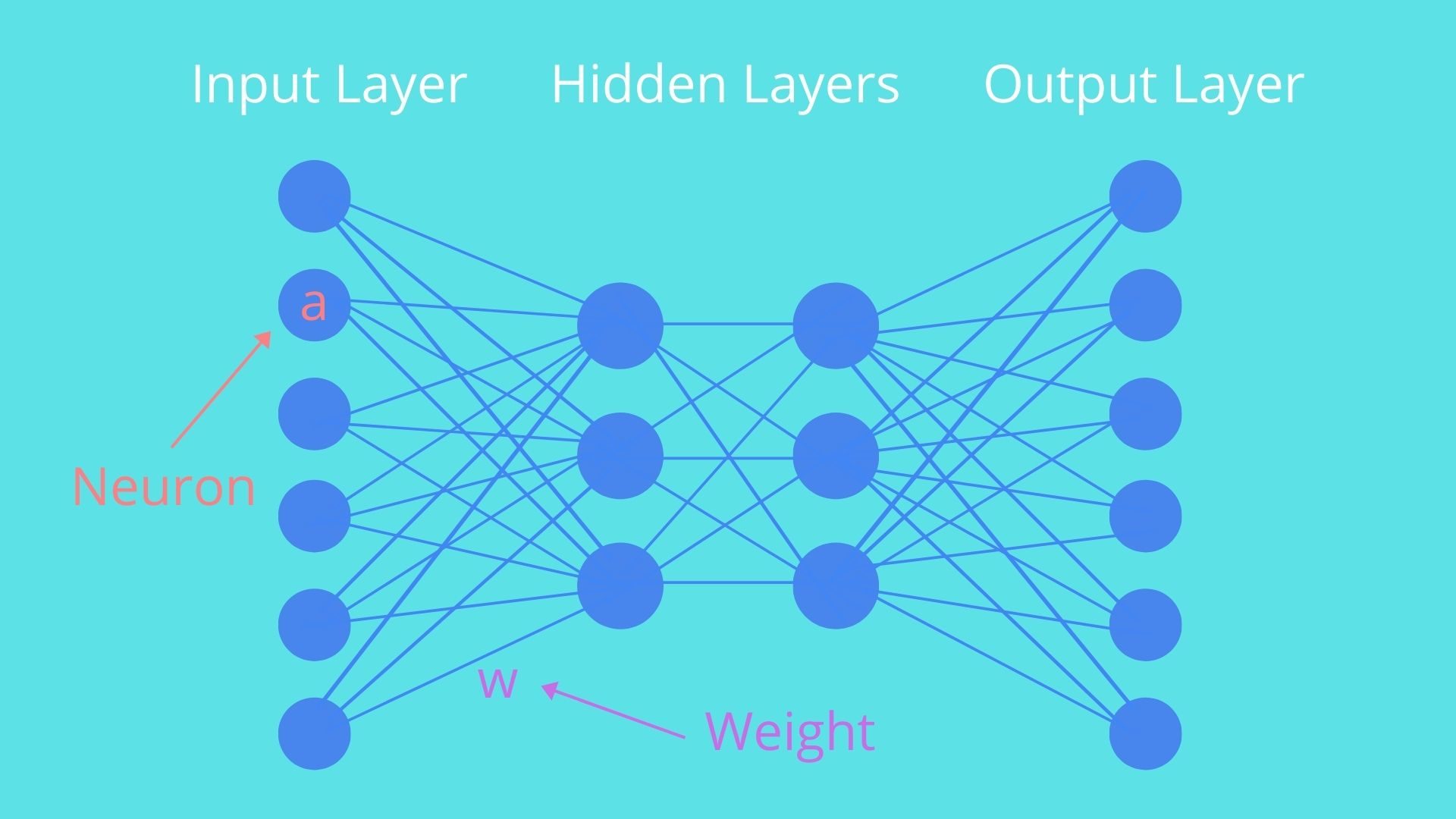
手書きの画像から数字を判定するためには、入力から出力までの間に何らかのプロセスがなくてはいけません。この間の部分を「隠れ層(Hidden Layers)」と呼びます。この層の構造は任意の選択が可能ですが、ここでは2層構造を想定し、それぞれの層はそれぞれ16ずつのニューロンから構成されているものとします。
重み(Weights)
元の画像のピクセルに対応する入力層のニューロンと隠れ層のニューロンの繋がりは、重み(weght)と呼ばれるパラメーターを使って表されます。重みもまた数字で、ある層のニューロンと次の層のニューロンを結ぶ一つ一つのラインに対応するそれぞれの値を持ちます。
隠れ層の1つ目の層にある一つのニューロンが、画像のある特定の領域に、丸や線を構成する要素があるかどうかをチェックする役割を担っているとすると、その要素がある部分には正の値を、その周辺のグレーのエッジがある部分には負の値を、それ以外には0の値を与えます。
入力層のニューロンの値と重みの値を掛け合わせるという計算をして、次の層の特定のニューロンの値を導いて行きます。
$$w_1a_1+w_2a_2+w_3a_3+…+w_na_n$$
シグモイド関数(Sigmoid Function)
この計算結果は様々な値をとることができますが、次の作業を進めるために結果を0から1の間のある値にしたいということになります。そこで、シグモイド関数と呼ばれるものを使って、この計算結果を0から1の間の値に変換します。
$$σ(x)=\frac{1}{1+e^{-x}}$$
この関数は、より大きな負の値を0に近づけ、より大きな正の値を1に近づけるという操作をするものです。これを使って重みを掛けた合計の値は以下のように表されます。
$$σ(w_1a_1+w_2a_2+w_3a_3+…+w_na_n)$$
バイアス(Bias)
このとき、どんな値でも0より大きい全ての場合にニューロンに点灯して欲しいという訳ではありません。より大きな値の場合のみ点灯するようにするために、バイアスと呼ばれるものを導入します。例えば、重みを掛けた合計の値が、10よりも大きい場合にのみ点灯するようにするためには、10という値のバイアス入れます。
$$σ(w_1a_1+w_2a_2+w_3a_3+…+w_na_n-10)$$
これが隠れ層の一層目で行われることになります。入力層のニューロンの数は784で、隠れ層一層目のニューロンが16でしたので、それぞれの関係の数だけ、つまり784x16=12544の重みがあることになります。またバイアスの数は16です。
よりシンプルな表現
上記の式はもっとシンプルに表すことができます。というのも上記の表現だと、一つ目の層から次の層にいく過程だけで、ものすごい数の式を書かなければいけなくなるためです。そこで、入力層の個々のニューロンの表現を線形代数のベクトルという概念を使ってひとまとめにし、また全ての重みを行列としてまとめて表現します。バイアスも同様にベクトルを使って表すようにします。その全体をシグモイド関数に当てはめると、次の層の全体像を表すことができます。
$$a^{(1)}=σ(Wa^{(0)}+b)$$
さらに次の層にいく過程でも同じことが行われます。つまり、隠れ層二層目のそれぞれのニューロンに対して、一層目のニューロンとの関係に応じた重みが設定され、上記と同じ作業を通して出力層のニューロンを点灯させるのです。
$$a^{(2)}=σ(Wa^{(1)}+b)$$
ニューラルネットワークはどのように学習するのか
学習(Learning)
ニューラルネットワークが学ぶというのはどういうことかというと、問題を解くのに必要な重みとバイアスの値を探すということを意味します。ここで問題と解くというのは「9」という手書きの数字が書かれた画像を入力したのであれば、9に対応する出力層のニューロンが最も明るく点灯するということを意味します。
もし、重みとバイアスをランダムに設定すると、出力層のランダムなニューロンが点灯する状態になります。一方、正確な判定ができるニューラルネットワークの場合は、出力層の正しい数字のニューロンのみが点灯する状態になります。
良いニューラルネットワークと悪いニューラルネットワーク
あるニューラルネットワークが、どれくらい良いニューラルネットワークであることを、数値で表すためには、悪いニューラルネットワークの出力層のそれぞれのニューロンの値から、正確な回答を出すニューラルネットワークの出力層のそれぞれのニューロンの値を引き、それぞれを2乗したものを足し合わせます。この合計をコストと呼び、その値が小さいほど判定が正確で、大きいほど不正確であることを示します。
コスト関数(Cost Function)
あるニューラルネットワークに何万という手書きの数字の書かれた画像を入力してコストの平均値を出します。その値がそのニューラルネットワークの良し悪しを測る基準となります。あるニューラルネットワークの、重みとバイアスをインプット(w)として、コストの平均値をアウトプット(C)として出す関数をコスト関数と呼びます。
$$C(w)$$
悪いニューラルネットワークを改善する
悪いニューラルネットワークだということが判明したら、それを改善するためにすべきことは、アウトプットであるコストの平均値を最小にする、重みとバイアスを見つけるということです。ではどのようにすれば最適な重みとバイアスが見つかるのでしょうか?微分を使えば、関数$C(w)$が最小値をとる$w$の値を見つけることができます!
$C(w)$を微分して出した接線の傾きが、右肩上がりであれば左に移動、左肩上がりであれば右に移動という操作を繰り返していけば、局所的に最小値になるところを見つけることができます。さらに傾きの度合いによって移動の度合いを調整すれば、最小値を通り過ぎることなく、グラフの谷間の部分に落ち着くことができます。
もちろんコスト関数はたくさんの入力値をもつ複雑なグラフを描く関数で、上がったり下がったりする曲線を描いているため、実際に見つかるのは局所的な最小値ということになります。
ニューラルネットワークを視覚的に理解する
ニューラルネットワークを理解するのに役立つリンクをいくつかご紹介しておきたいと思います。
3BLUE1BROWN
私は「3BLUE1BROWN」というYouTubeチャンネルのファンなのですが、ニューラルネットワークを視覚的に非常にうまく表現したビデオがあります。解説は英語ですが、図を見るとニューラルネットワークの概念がよくわかると思いますので、この記事と合わせて参考にしてみてください。
Deeplearning.ai
こちらは人工知能研究と教育で有名なAndrew Ng氏のYouTubeチャンネルにあるプレイリスト。上記のものに比べると専門的になりますが、両方合わせてみるとより理解度が増します。





