わかりやすいアインシュタインの特殊相対性理論

私たちが「相対性理論」として認識している理論には実は２つのものがあります。１つが特殊相対性理論と呼ばれるもので、もう一つが一般相対性理論と呼ばれるものです。特殊相対性理論と一般相対性理論が異なるのは、重力を考慮しているかという点においてです。一般相対性理論が複雑な数学を要するのに対して、特殊相対性理論は比較的簡単な数学で内容を理解することができます。

特殊相対性の２つの仮定

１９０５年に発表されたアインシュタインの特殊相対性理論は２つの仮定から導かれています。この仮定は、英語でpostulates of special relativityと呼ばれるものです。

１つ目の仮定：相対性原理

１つ目の仮定は「相対性原理（the principle of relativity）」とも呼ばれるもので、「物理学の法則は、すべての慣性座標系（inertial frames of references）において同じである」というものです。

慣性座標系というのは、ある運動の基準となる枠組み、あるいはフレームのことです。例えば、駅のプラットフォームいる人と、駅を通過する電車に乗っている人では、ものの動きが異なって見えます。プラットフォームに置かれたベンチは、プラットフォームにいる人から見れば静止しているように見えますが、動いている電車の中にいる人から見ると、電車がプラットフォームを通り過ぎると後ろに向かって遠ざかっていくように見えますね。

このような場合、プラットフォームにいる人と、電車に乗っている人は異なる慣性座標系にあるものとして考えるのです。「慣性座標系」というと難しく聞こえますが、英語を見るとわかるように、「参考にする枠組み」ということなので、駅や電車を「フレーム」として考えてみるとわかりやすいと思います。それぞれの慣性座標系において、物理学の法則は同様に有効であるということになります。

２つ目の仮定：光速度不変の原理

２つ目の仮定は「光速度不変の原理（invariance of c）」と呼ばれるもので、「真空での光の速度はすべての慣性座標系において同じであり、光源の運動にはよらない」というものです。

例えば、秒速1000メートルで動いている宇宙船を地球から観察しているとします。この宇宙船から見て秒速2000メートルのミサイルが発射されたとすると、地球から見たミサイルの速度は、

1000＋2000＝秒速3000メートル

ですね。でも、ここで同じ宇宙船から速度cの光のビームが発射されたとします。上記と同じように考えると、地球から見た光のビームの速度は、秒速1000＋cメートルとなるような気がしますが、先ほどの光速度不変の原理を考慮するとそうはならず、なんと地球から見た光のビームの速度もcなのです！

観察者は光速を超えられない

地球から見た光のビームの速度がcとなるためには、以下の２つの可能性が考えられます。

①地球から見た宇宙船の速度が0で、宇宙船から見た光のビームの速度がcの場合。つまり、地球から見た光のビームの速度は0＋c＝cになります。

②地球から見た宇宙船の速度がcで、宇宙船から見た光のビームの速度が0の場合。つまり、宇宙船が光速で移動しているために、宇宙船と光のビームが一緒にしている状態になり、よって地球から見た光のビームの速度は、c＋0＝cになります。

光速度不変の原理によると、宇宙船から見た光のビームの速度もcである必要があります。よって②は不可能ということになります。どの慣性座標系から見ても光速が一定ということは、「ある慣性座標系にいる観察者は、真空中での光速を超えることはできない」ということを意味します。つまり、宇宙船に乗っている宇宙飛行士は光速で移動することはできないのです。

①に関しても、地球から見た宇宙船の速度が秒速1000メートルだったことと矛盾していますね。アインシュタインの２つの仮定は、私たちの日常的な体験とは相反しているように感じられます。経験的に理解できる①の可能性も②の可能性否定されてしまうのですから、一体どうなっているのか理解できない！という人もいるでしょう。でも、実験結果が自然界の現象はこうなのだということを示しているので、私たちはそういうものとして受け止めるしかないのです。

時間の拡張

ある慣性座標系S’の空間の同じ場所で２つの事象が起こるとき、その２つの事象が起こる時間の間隔を固有時間（proper time interval）と呼び、$Δt_0$で表します。この系S’がもう一つの慣性座標系Sに対して一定速度uで動いているとき、この系Sにおいて観察される２つの事象が起こる時間の間隔$Δt$は、$Δt_0$よりも長くなります（time dilation）。ではなぜ動いていると時間の間隔は長くなるのでしょう？

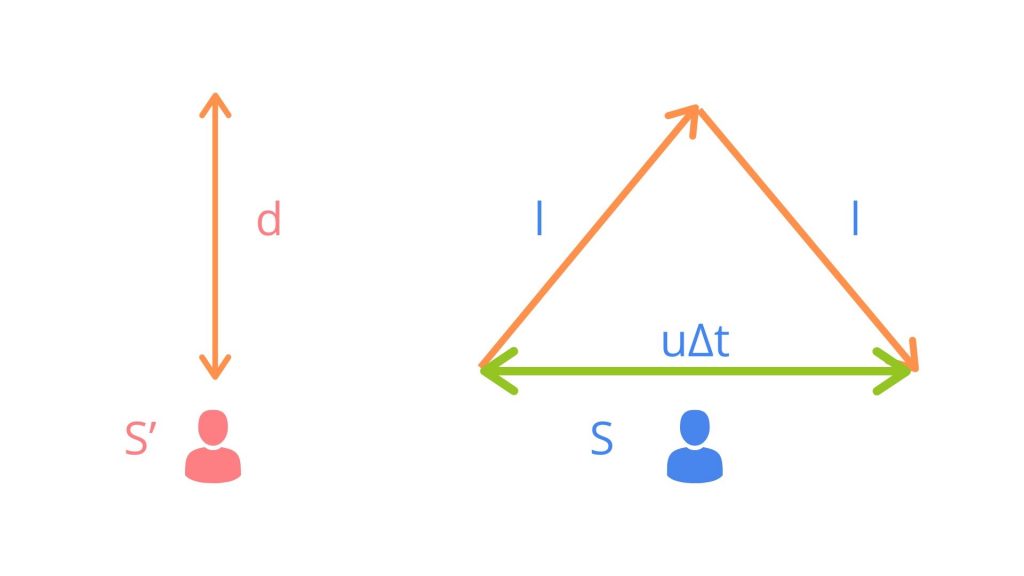
座標系S’での固有時間

例えば、座標系S’を一定速度uで動いている電車、座標系Sを駅のプラットフォームとして考えます。電車の床に光源を置き、電車の天井に貼りつけた鏡に光が当たって光源に戻ってくるまでのS’における固有時間を$Δt_0$とします。光源から鏡までの距離をdとすると固有時間は、

$$Δt_0=2d/c$$

と表すことができます。

座標系Sから観察した時間

一方、同じ光の運動を駅のプラットフォームから観察した場合、$Δt$は次のように記述することができます。

$$Δt=2l/c$$

ここでlは、光が光源から鏡を経て光源に戻ってくるまでの移動距離で、dよりも長くなります。ピタゴラスの定理よりlは以下の式で表すことができます。

$$l=\sqrt{d^2+(uΔt/2)^2}$$

２つの系の時間の関係

ここから、

$$Δt=2/c\sqrt{(cΔt_0/2)^2+(uΔt/2)^2)}$$

$$=\frac{Δt_0}{\sqrt{1-u^2/c^2}}$$

という２つの系の時間$Δt$と$Δt_0$の関係を導くことができます。

$$γ=\frac{1}{\sqrt{1-u^2/c^2}}$$

で表されるγを定義して、

$$Δt=γΔt_0$$

と表されることもあります。つまり、γの値の分だけ時間が拡張されているということになります。

長さの収縮

ある慣性座標系S’において２つの点が静止していて、２点間の長さがその系の中で測られるとき、この長さを固有長（proper length）と呼び、$l_0$で表します。この座標系S’がもう一つの慣性座標系Sに対して一定速度uで動いているとき、この長さが系の動きと平行方向にその長さが測られると、座標系Sで測られた長さは$l$は、$l_0$よりも短くなります（length contraction）。

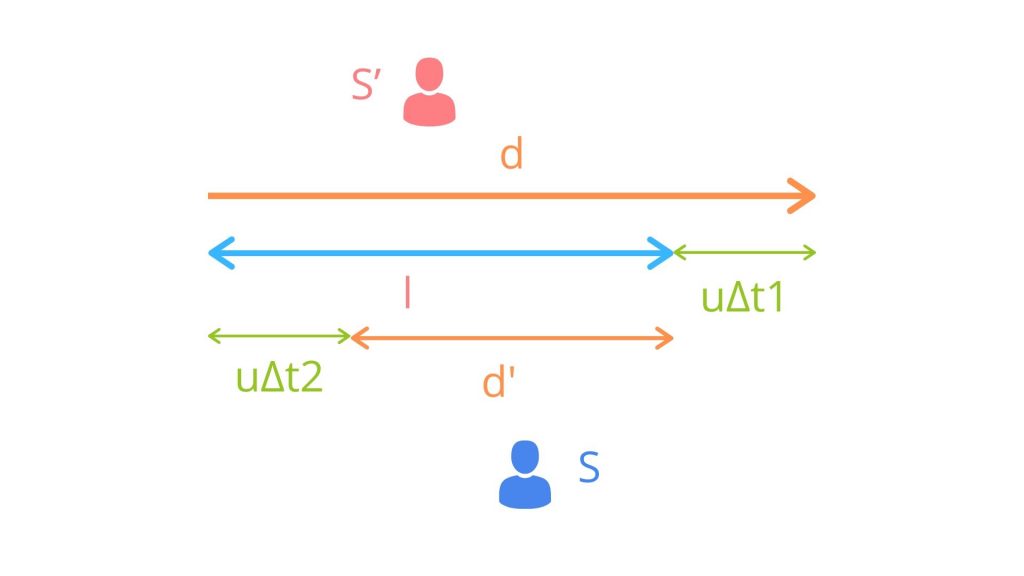
座標系S’の固有時間

先ほどと同様に、座標系S’を一定速度uで動いている電車、座標系Sを駅のプラットフォームとして考えます。電車の中にある長さ$l_0$のものさしの片方の端に光源を置き、反対側の端に鏡を置きます。ものさしは座標系S’に対して静止しているものとします。光が光源を出て、鏡に当たって跳ね返り、光源まで戻ってくるまでにかかる時間$Δt_0$は、以下の式で表すことができます。

$$Δt_0=2l_0/c$$

この時間$Δt_0$は、光の出発点と終着点がこの系の空間において同じ場所にあるので固有時間になります。

座標系Sから観察した光源から鏡までの時間

今度はこれをプラットフォームから観察することを考えてみましょう。

座標系Sから見た電車の中のものさしの長さをl、系Sで測った光が光源から鏡までに行き着くのにかかる時間を$Δt_1$とします。

この時間$Δt_1$の間に、電車に乗ったものさしは$uΔt_1$の距離を移動します。すると、光が鏡までに行き着くのに辿った距離dは、lではなく

$$d=l+uΔt_1$$

ということになります。また、この距離dは光が時間$Δt_1$の間に進んだ距離でもあるので、

$$d=cΔt_1$$

と表すことも出来ます。この２つの式から以下の関係を導くことができます。

$$Δt_1=l/c-u$$

座標系Sから観察した鏡から光源までの時間

同様に、鏡から光源まで戻るのにかかる時間$Δt_2$を求めることが出来ます。この時間$Δt_2$の間に、電車に乗ったものさしは$uΔt_2$の距離を移動します。すると、光が鏡までに行き着くのに辿った距離d’は、

$$d=l-uΔt_1$$

と表すことが出来ます。上記と同様に$d=cΔt_2$と表すこともできることから、以下の式が成り立ちます。

$$Δt_2=l/c+u$$

座標系Sから観察した往復時間

座標系Sから観察した場合に、光が光源から鏡を経て再び光源に戻るのにかかる時間$Δt$は$Δt_1+Δt_2$より、

$$Δt=2l/c(1-u^2/c^2)$$

と表すことができます。

２つの系の長さの関係

２つの系の時間の関係が$γ=1/{\sqrt{1-u^2/c^2}}$で表されたことから、$Δt_0$と$Δt$にそれぞれ上記の式を代入して整理すると、２つの系の長さ$l_0$と$l$の関係を得ることが出来ます。

$$l=l_0\sqrt{1-u^2/c^2}=l_0/γ$$

つまり、γの分だけ長さが収縮しているということになります。

エネルギーと質量の等価性

相対論というと、$E=mc^2$ という有名な式を見たことがあるのではないでしょうか？その導出について簡単に触れておきたいと思います。

相対性理論の特筆すべき結果の一つが、エネルギーと質量の等価性を示す有名な方程式 $E=mc^2$ です。この式は、質量とエネルギーが相互に変換可能であることを意味しています。

運動エネルギーの再考

ニュートン力学では、運動エネルギーは以下の式で表されます。

$Ek=12mv2E_k = \frac{1}{2}mv^2 $

特殊相対性理論では、この式が修正され、エネルギーと運動量の関係が次のように記述されます。

$E2=(pc)2+(m0c2)2E^2 = (pc)^2 + (m_0c^2)^2 $

ここで、

$E$ は系全体のエネルギー。
$p$ は運動量。
$m_0$ は静止質量。

運動量 $p$ は、次のように表されます。

$p=γm0vp = \gamma m_0v $

また、$\gamma$ は以下のように定義されます。

$γ=11−v2c2\gamma = \frac{1}{\sqrt{1 – \frac{v^2}{c^2}}} $

静止質量エネルギー

物体が静止している場合、つまり速度 $v = 0$ の場合には運動量 $p = 0$ となります。このとき、エネルギーの式は以下のようになります。

$E=m0c2E = m_0c^2 $

この結果は、静止している物体がエネルギーを持つことを示しています。このエネルギーは「静止エネルギー」と呼ばれ、$m_0c^2$ によって与えられます。

全エネルギーの一般式

物体が運動している場合には、エネルギー $E$ は運動エネルギー $E_k$ と静止エネルギー $m_0c^2$ の和として次のように表されます。

$ E=γm0c2E = \gamma m_0c^2 $

この式は、運動エネルギーの観点から特殊相対性理論を考える基礎となります。速度が小さい場合（$v \ll c$）、$\gamma$ をテイラー展開すると、ニュートン力学の運動エネルギーに近似できます。

テイラー展開について

テイラー展開とは、関数をある点の周りで多項式として近似する方法です。たとえば、$\gamma = \frac{1}{\sqrt{1 – \frac{v^2}{c^2}}}$ を展開すると次のようになります（$v \ll c$ の場合）：。

$γ≈1+12v2c2+38v4c4+…\gamma \approx 1 + \frac{1}{2}\frac{v^2}{c^2} + \frac{3}{8}\frac{v^4}{c^4} + \dots $

この近似を用いると、運動エネルギーの低速領域での挙動がニュートン力学と一致することが確認できます。つまり、

$ Ek=(γ−1)m0c2≈12m0v2E_k = (\gamma – 1)m_0c^2 \approx \frac{1}{2}m_0v^2 $

となり、ニュートン力学の結果が導かれます。

質量とエネルギーの等価性の意義

式 $E = m_0c^2$ は、質量がエネルギーの形で蓄えられていることを示しています。これは、質量がエネルギーに変換可能であり、その逆もまた可能であることを意味します。この原理は、核エネルギーや素粒子物理学において極めて重要です。たとえば、核分裂や核融合では、質量の一部がエネルギーとして放出されます。