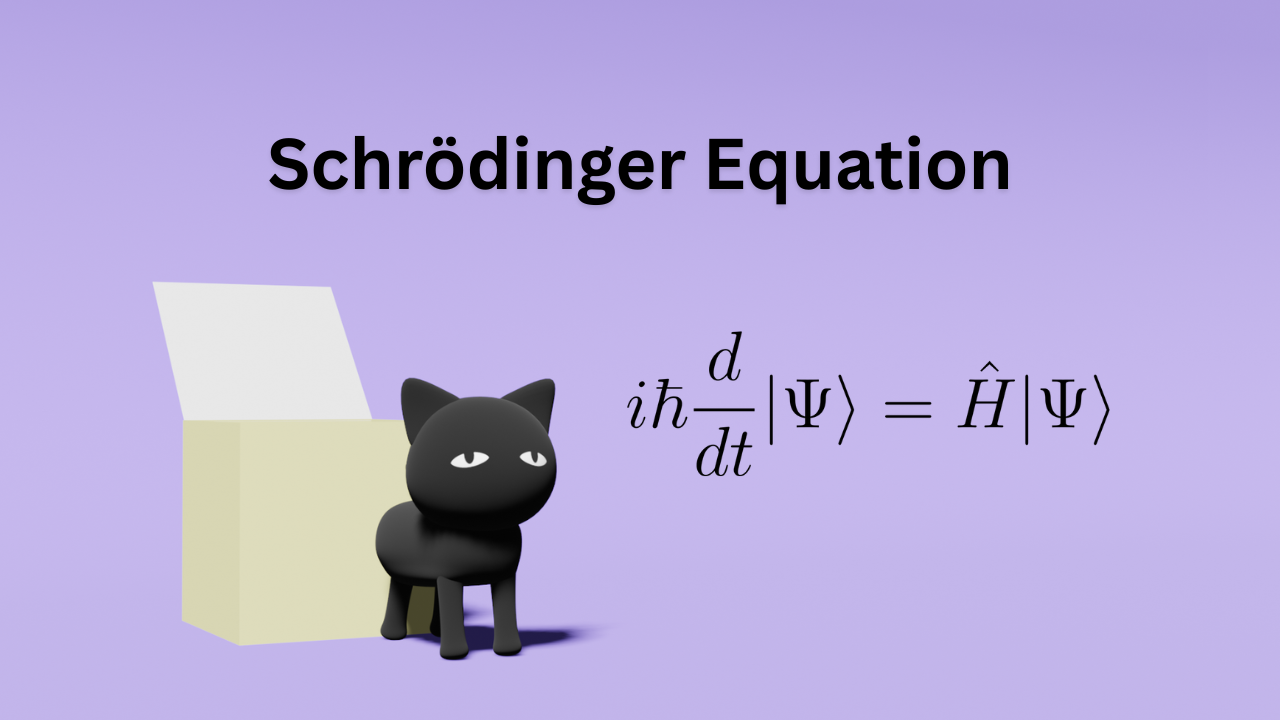量子力学の基礎的な方程式であるシュレディンガー方程式。「シュレディンガーの猫」というポピュラーな思考実験もあって、シュレディンガーの名前を聞いたことのある人は多いと思います。でも、その中身について理解するのはなかなか難しいかもしれません。
かのリチャード・ファイマンが「I think I can safely say that nobody understands quantum mechanics. (量子力学を理解している人などいないと私は安心して言うことができると思う)」と言ったくらいですから、それは当然のことでしょう。
この記事では、高校までの物理や数学の知識で理解できるように順を追って、できるだけわかりやすくシュレディンガー方程式について説明してみたいと思います!
ちなみに、シュレディンガー方程式をモチーフにしたTシャツなどの科学グッズを作ってみました。下の写真以外にもTシャツはいろんな色から選べるので、ぜひ以下のリンクからSuzuriのショップを覗いてみてくださいね。Tシャツ以外にも、スマホケースやバッグなどの小物もありますよ。
シュレディンガー方程式とは
まず、シュレディンガー方程式とはどんなものなのでしょう?
シュレディンガー方程式は、オーストリア人物理学者エルヴィン・シュレディンガーによって1926年に発表された量子力学の基礎となる方程式で、以下の式がシュレディンガー方程式です。
$$iℏ\frac{∂ψ(x, t)}{∂t}=-\frac{ℏ^2}{2m}\frac{∂^2ψ(x, t)}{∂x^2}+Vψ(x, t)$$
量子と呼ばれる電子や光子のような小さな物体は、粒子としての性質と波としての性質の両方を持ち合わせています。
その波を波動関数と呼ばれる関数で表し、その関数が従うべき物理学上のルールをエネルギーや運動量という粒子の性質と共通する属性を介して数学的に記述しようとしたのがシュレディンガー方程式です。
シュレディンガー方程式の解である波動関数ψは、ある場所でその量子が検出される「確率」を表すものです。確率ですから必ずしもそこにあるというわけではなく、全く別のところで検出される可能性もありますが、そこで検出される確率が高いということになります。
この記事ではできるだけわかりやすくするために3次元ではなく1次元の式で話を進めたいと思います。下のような形の式をシュレディンガー方程式として見たことのある人もいるかもしれません。
$$iℏ\frac{∂ψ}{∂t}=\hat{H}ψ$$
一般的にはこのように表されますが、より身近な表現を使ってわかりやすくシュレディンガー方程式について知るために、最初の式にを元に話を進めていきます。
私たちが中学校や高校で習った物理や数学の知識を総動員してこの方程式を見てもピンと来ないのは、
- ℏ(エイチ・バーと読みます)という定数
- 変数が2つ入ったψ(サイと読みます)という関数
- ∂を使って表された偏微分
- 虚数i
といったものが登場しているからではないでしょうか。目に見えている物理的なものを構成する粒子について話しているのに、虚数が出てくるのはどういうこと?と思ってしまいますよね。
でも逆に言えば、この式の導出をそれぞれの要素を理解しながら見ていけば、この方程式の意味がわかるようになると思いませんか?辛抱強く、順を追って見て行きましょう。
物質は波である
粒子と波
私たちが、直感的に物質の運動を捉える際にイメージしているのは、粒子ではないでしょうか?例えば、車の速度や、ボールを投げた時の軌道などについて考える時、私たちは質点について考えます。車やボールを波としてイメージしている人はおそらくあまりいないですよね。
一方、X線やマイクロ波などの電磁波は、その名の通り個別の粒子ではなく、海の波と同様に連なって伝播していく波として捉えているのではないでしょうか?この粒子と波という2つの異なるコンセプトが量子力学ではとても重要になります。
ド・ブロイ波
17世期に生まれた偉大な科学者ニュートンは光を粒子だと考えていましたが、その後の時代のマックスウェルらの仕事によって、光は電磁波の一種として波と考えられるようになっていました。
ところが、光のエネルギーが連続ではなく飛び飛びの値をとる、つまり光が粒子のような振る舞いをすることがわかると、これまで粒子と考えられていた電子もまた、波のように振る舞うのではないかと考えられるようになりました。このような光の粒子を光子と呼びます。
物質が波として振る舞うという考えの考案者はルイ・ド・ブロイと言うフランス人物理学者です。彼の名にちなんでこのような物質の波の性質はド・ブロイ波、あるいはド・ブロイの物質波と呼ばれています。つまり、電子や光子は粒子としての性質と、波の性質の両方を兼ね備えているということになります。
すると、光子や電子を司る波がどんな波なのか知りたくなりませんか?その波を波動関数と呼ばれる関数で表し、その関数が従うべき物理学上のルールをエネルギーや運動量という粒子の性質と共通する属性を介して数学的に記述しようとしたのが、シュレディンガー方程式というわけです。
波動関数
海の波や音の波を数学的に表現するために、波動関数と呼ばれる関数の式が使われることについては、別の記事で説明しています。ド・ブロイ波も波ですから、同様に波動関数を使うことができます。波動関数について馴染みのない方は波の性質と波動関数をわかりやすく説明した記事がありますので、そちらを先にご覧ください。
上記の記事では、波動関数をx軸とy軸を使ってy(x, t)として表しましたが、ここではシュレディンガー方程式で通常使われる「ψ(サイ)」と言う記号をyの代わりに使って進めていきたいと思います。ψ(x, t)は記号が変わっただけで基本的にy(x, t)と同じことで、位置xと時間tの関数です。波が三次元的に伝播する場合は、この関数の位置についての変数をxだけでなくx、y、zと3方向にとることができますが、まずは話をわかりやすくするために一次元的な波を考えていきます。
ド・ブロイ波を表す波動関数は以下のように表すことができます。
$$ψ(x, t)=Acos2π(\frac{x}{λ}-νt)$$
ここで、xは波の上のある一つの場所、tは時間、Aは振幅、λは波長、νは振動数を表しています。サインやコサインのグラフが波を表すことは文系の人も高校で習いましたよね。ですから、波を表す式がコサインの関数になるというのは比較的簡単にイメージできると思います。
これで、まず最初の疑問だったシュレディンガー方程式に登場する「ψ(サイ)」の意味がわかりましたね。ψはド・ブロイ波、つまり波としての物質の振る舞いを記述する波動関数ということになります。では、この波動関数はどんな条件を満たす必要があるものなのでしょう?
エネルギーと運動量
光について、エネルギーEと運動量pはそれぞれ、その振動数νや波長λと以下の式によって結び付けられています。
$$E=hν$$
$$p=\frac{h}{λ}$$
ここでhはプランク定数と呼ばれる定数です。つまりエネルギーは振動数に比例するということになりますね。紫外線は赤外線に比べて、波長が短く、振動数が大きいため、肌に与えるダメージが大きい、つまりエネルギーが大きいことを考えてもらうと、波とエネルギーの関係のイメージが湧くと思います。
光は電場と磁場で構成される電磁波と呼ばれる波であることがマックスウェルによって示されていましたが、アインシュタインは金属に光を照射すると光からエネルギーを得た電子が金属の外に飛び出すことから、光もまた波の性質を持つと同時に粒子であると考えました。この性質について馴染みのない方は、光電効果についてわかりやすく説明した別の記事も参考にしてください。
粒子であるならボールが運動量を持つのと同様に、光もまた運動量を持つと考え、光の運動量を求めました。それが上記のpで表される式です。
波動関数を書き換える
波長λと周波数νを使って書かれていた先ほどの波動関数ψの式を、運動量pとエネルギーEを使って書き換えてみると以下のようになります。
$$ψ(x, t)=Acos2π(\frac{px}{h}-\frac{Et}{h})$$
これは単に代入して書き換えただけなので問題ないですね。
わかりやすいシュレディンガー方程式についての本はこちらをご覧ください。
物質は粒子でもある
運動エネルギーと位置エネルギー
ここで再び、粒子として性質について考えてみましょう。私たちが粒子を扱う時に考えたように、物質の持つエネルギーEは、運動エネルギーTと位置エネルギーVを合わせた量なので、以下のように書くことができます。KとUという記号を使っていたかもしれませんが、高校でも習いましたね。
$$E=T+V$$
運動エネルギーTは物体の質量mと速度vを使って$T=\frac{1}{2}mv^2$と表すことができるので、エネルギーEを以下ように書き換えることができます。
$$E=\frac{1}{2}mv^2+V$$
さらに、粒子の運動量は$p=mv$と表すことができることから、エネルギーは以下の式に変形することができます。
$$E=\frac{p^2}{2m}+V$$
波であり粒子であるという性質
「波であると同時に粒子でもある」という量子の性質を記述するためには、先ほど書き換えた波動関数が、上記の式を満たせば良いということになります。ここで、波の振る舞いを表す式と、粒子の振る舞いを表す式の両方に、エネルギーEと運動量pという項があることに注目していただきたいと思います。これを使って、2つの式を合体することができそうです。
ただ、これらを合わせるためにEとpに代入できるようにするには波動関数の式をもう少し変形する必要がありそうです。
便利なオイラーの公式
Eとpを取り出すためには、どうすれば良いのでしょうか?波動関数のコサインの式をxで微分すると、pを括弧の外に出すことができ、またtで微分するとEを括弧の外に出すことができます。ただ、コサインの式を微分すると、サインになってしまうのがちょっと面倒ですね。
オイラーの公式とは
実は、そんな時にとっても便利な公式が存在しています。それは、以下に示したオイラーの公式と呼ばれるものです。
$$e^{iθ}=\cos{θ}+i\sin{θ}$$
ここで登場した「e」 はネイピア数と呼ばれる数です。2.71・・・と値のある数ですが、πのように数学的に便利な数としてよく使われ、eという記号で表されます。
ネイピア数eは自然対数の底で、ネイピア数を底とする指数関数は何回微分しても変わらないという性質があります。つまり以下が成り立ちます。
$$\frac{d}{dθ}e^{θ}=e^{θ}$$
微分しても元の指数関数のままですね。xの前に係数がつく場合は、通常の指数関数の微分と同じで以下のようになります。
$$\frac{d}{dθ}e^{aθ}=ae^{aθ}$$
何回微分しても変わらないという特性は、私たちがやろうとしていた波動関数から運動量とエネルギーを取り出そうとするのに非常に便利そうですよね。
ネイピア数を使った波動関数の表現
オイラーの公式$e^{iθ}=\cos{θ}+i\sin{θ}$を見てみると、実部がコサイン、虚部がサインとなっています。先ほど私たちが見ていた波動関数は、
$$ψ(x, t)=Acos2π(\frac{px}{h}-\frac{Et}{h})$$
とコサインの式で表されていましたが、私たちが海や音の波を扱うときに実際に知覚しているのが実数の世界でのことで、波動関数には虚数の世界に対応する部分があるとしたら、波動関数をより一般的に記述するために以下のように表すことができます。
$$ψ(x, t)=Acos2π(\frac{px}{h}-\frac{Et}{h})+iAsin2π(\frac{px}{h}-\frac{Et}{h})$$
するとオイラーの公式を使って、波動関数ψ(x, t)をネイピア数eを底にした指数関数として書き換えることができます。
$$ψ(x, t)=Ae^{\frac{2πi}{h}(px-Et)}$$
エネルギーEを求める
指数関数として置き換えた波動関数ψ(x, t)を、Eについての式にすることを考えてみましょう。どうすれば良いかというと、時間tについて偏微分すると、指数に含まれているEが前に出てきます。偏微分というのは、変数が複数ある関数に置いて、ある一つの変数についてのみ微分することです。それ以外の変数は定数とみなして構いません。つまり、この式を時間tのみについての関数とみなし、tについて微分するということになります。
$$\frac{∂ψ}{∂t}=-\frac{2πi}{h}EAe^{\frac{2πi}{h}(px-Et)}=-\frac{2πi}{h}Eψ$$
ここで、係数が煩わしいので、エイチ・バーと呼ばれる数を以下のように定義します。
$$ℏ=\frac{h}{2π}$$
$\frac{h}{2π}$の代わりにℏを使って上記の式を表わすために、両辺に−iℏかけて整理すると以下の式を得ることができます。
$$iℏ\frac{∂ψ}{∂t}=Eψ$$
運動量pを求める
上記と同様に、指数関数として置き換えた波動関数ψ(x, t)を、今度は位置xについて偏微分すると、以下のような関係を得ることができます。
$$iℏ\frac{∂ψ}{∂x}=pψ$$
ここでは、pの2乗を得たいので、さらにもう一回偏微分すると以下のような式を得ることができます。何回微分しても変わらないネイピア数の性質がここで生きていますね。
$$-ℏ^2\frac{∂^2ψ}{∂x^2}=p^2ψ$$
エネルギーと運動量の書き換え
ちなみにエネルギーEと運動量pは、波の性質に基づいて以下のような書き換えが可能です。以下の表で、fは振動数、vは速度、ωは角振動数、λは波長、kは波数です。(νとvが紛らわしく見えることから、ここでは振動数をνではなくfと書きました。)
| エネルギーE | 運動量p |
|---|---|
| $E=hf$ | $p=h/λ$ |
| $E=hv/λ$ | $p=hv/f$ |
| $E=ℏ2πf$ | $p=ℏ2π/λ$ |
| $E=ℏω$ | $p=ℏk$ |
| (プランクとアインシュタインの関係) | (ドブロイの関係) |
ちょっと難しいオイラーの公式の話をして、少しお疲れかもしれません。そんなみなさんのためにこんな動画も作ってみました。シュレディンガーの猫の気持ちがわかるかもしれません。ぜひご覧ください。よろしければ、いいねとチャンネル登録もお願いします!
エネルギーの式に代入する
一次元シュレディンガー方程式
これが最終段階の手順になります。以下の運動エネルギーと位置エネルギーの式の両辺に、
$$E=\frac{p^2}{2m}+V$$
ψ(x, t)をかけて上記で求めたエネルギーと運動量を代入しやすくします。
$$Eψ=\frac{p^2}{2m}ψ+Vψ$$
ここに$p^2ψ$と$Eψ$を代入すると以下の式が出来上がります。
$$iℏ\frac{∂ψ(x, t)}{∂t}=-\frac{ℏ^2}{2m}\frac{∂^2ψ(x, t)}{∂x^2}+Vψ(x, t)$$
これで一番最初にご紹介したシュレディンガー方程式が完成しました。導出過程を考えてみると、左辺がエネルギーの総和、右辺の第一項が運動エネルギー、第二項が位置エネルギーであることがわかると思います。
三次元シュレディンガー方程式
ここまで話をわかりやすくするために、ド・ブロイ波がx軸の方向にのみ動くものとして考えてきましたが、これを三次元に拡大するためにx軸だけでなく、y軸、z軸も取るとすると、波動関数は$ψ(x, y, z, t)$となり、シュレディンガー方程式は以下のように書くことができます。
$$iℏ\frac{∂ψ}{∂t}=-\frac{ℏ^2}{2m}[\frac{∂^2ψ}{∂x^2}+\frac{∂^2ψ}{∂y^2}+\frac{∂^2ψ}{∂z^2}]+Vψ$$
シュレディンガー方程式の意味
シュレディンガー方程式の解
ここまでは方程式の導出について考えてきましたが、シュレディンガー方程式を解くとその解は波動関数ψということになります。この波動方程式はある物質の振る舞いを表す関数です。ただ厄介なのは、量子を検出しようとすると実態のある粒子として観察される一方で、検出されるまではその振る舞いが波として表されるという点です。これは一体どういうことなのでしょうか?
確率的解釈
シュレディンガー方程式の解である波動関数ψは、ある場所でその量子が検出される「確率」を表すものです。確率ですから必ずしもそこにあるというわけではなく、全く別のところで検出される可能性もあります。そしてその確率は$|ψ|^2$に比例します。これを確率密度と呼び、ρで表します。
$$ρ=|ψ|^2$$
ここで、より一般的な波動関数ψを複素関数で表したことが意味を帯びてきます。というのは、
$$ψ=a+bi$$
とすると、実軸に対して対称な複素共役である$\bar{ψ}$というもう一つの複素関数は、以下のように表すことができます。
$$\bar{ψ}=a-bi$$
すると、$i^2=-1$によって、
$$ρ=ψ\bar{ψ}=|ψ|^2$$
が成り立ちます。つまり、物質の波の性質を表す波動関数が複素関数であることは、単なる数学的な操作ではなく必然ということになってきます。でも、虚数で表されるものの物理的な実体というのは誰にもわかりません。それは量子の世界の不可解な部分でもあります。それでもこの方程式に含まれる虚数は副次的なものではなく、本質的なものだと言われています。
わかりやすいシュレディンガー方程式についての本はこちらをご覧ください。
シュレディンガーの猫
シュレディンガーの猫というのもこの確率的解釈とリンクしています。シュレディンガーの猫は有名な思考実験で、量子の振る舞いによって毒ガスが発生する仕掛けの不透明な箱の中に猫がいるとします。量子の振る舞いは確率的なので、毒ガスは50%の確率で発生するとしかいうことが出来ません。毒ガスが発生すれば猫は死んでしまいますが、発生しなければ猫は生きています。でも箱を開けるまで、猫の状態はわかりません。量子の振る舞いを確実に知ることは出来ないからです。
「箱を開ける」というのは実験で量子を検出するということと対応しています。量子を検出するまで、量子の状態を正確に知ることは出来ず、それまでは猫が死んだ状態と生きた状態の重ね合わせにあると解釈されるのです。
量子力学的な波は、シュレディンガー方程式に従います。実際量子の世界の様々な実験結果が、この方程式に従っています。ニュートンの運動方程式が、ボールの動きのような私たちの身の回りの物体の振る舞いを記述する基礎的な方程式であるのと同様に、シュレディンガー方程式は量子の振る舞いを記述する基礎的な方程式なのです。
冒頭でご紹介したハミルトニアンを使ったデザインの他、このページで説明している1 次元の時間依存シュレディンガー方程式をモチーフにしたTシャツなどのグッズも作ってみました。ぜひSuzuriのショップを覗いてみてくださいね。Tシャツは特に大好評で多くの注文をいただいています!
他にも科学をテーマにしたデザインのグッズを作っていますので、ぜひ以下のページもご覧ください。