海の波、弦の振動、電磁波、音など身の周りには様々な波がありますが、いくつかの概念を理解すれば波を比較的シンプルな数式で表すことができます。この記事では、数式も使いますが文系の高校レベルの知識でもわかるように、図も踏まえながら順を追って見ていきたいと思います。シュレディンガー方程式を理解する一歩でもありますので、ぜひ最後まで読んでみてください。
ちなみに、このページで解説している波動方程式をモチーフにした科学グッズを作ってみました。シュレディンガーのネコのグッズなどもありますので、ぜひサイエンスデザインのページも覗いてみてくださいね。
2種類の波
波には大きく分けて2つの種類があります。横波(Transverse Waves)と呼ばれるものと、縦波(Longitudinal Waves)と呼ばれるものです。
横波(Transverse Waves)

海の波、電磁波、弦の振動、光などは横波です。横波の上がっている一番高い部分を山(crest)、下がっている一番低い部分を谷(trough)と言います。
横波の特徴として、波の伝達(propagation)の方向と、波の上にある粒子の振動(oscillation)の方向が直角(perpendicular)であるという特徴があります。
浮き輪をつけて海にぷかぷか浮いていることを考えてみてください。波が押し寄せて来ると、上下に上がったり下がったりしますが、波と共に水平方向に移動するということはありません。
縦波(Longitudinal Waves)

一方、音の波は縦波になります。縦波の場合、波の伝達の方向と、波の上にある粒子の振動の方向が平行であるという特徴があります。
横波では上に上がる山(crest)と下に下がる谷(trough)の対比がありましたが、縦波では密度が高くなる「密」(compression)と密度が低くなる「疎」(rarefaction)の対比で波が出来ています。
このような縦波も、グラフで示す場合は便宜的に横波と同じ波の図で示します。このとき、図の波の山の部分が密に対応し、谷の部分が疎に対応するものとして表現されます。
波に関する量とその関係
基本的な4つの量
波に関する重要な量には以下の4つがあります。
振幅(amplitude):平行状態からの最大のずれ幅を表します。単位はメートルで、記号ではAで表されます。
波長(wavelength):波の山から次の山まで(これを1つの波と考えます)の長さを表します。単位はメートルで、記号ではλで表されます。
周期(period):ある一点を波の山が通ってから次の山が通過する(つまり1つの波が通過する)までにかかる時間を表します。単位は秒で、記号ではTで表されます。
周波数(frequency):1秒間に通過する波の数を表します。単位はヘルツで、記号ではfで表されます。振動数と呼ばれることもあります。
周期と周波数の関係
周期Tと周波数fには以下の関係が成り立ちます。
$$T=1/f$$
$$f=1/T$$
fは1秒間にある一点を通過する波の数でした。1秒間に5つの波が通過するとすると$f=5$(ヘルツ)ですね。では1つの波が通過するのにかかる時間は何秒かと考えてみると、もちろん5分の1秒、$T=1/f$(秒)というわけです。
波の速度
波の速度は以下の式で表すことが出来ます。
$$v=fλ$$
つまり、波の速度(m/s)は周波数(1/s)と波長(m)の積(product)に等しいということになります。
光を含む電磁波の速度は一定なので、上記の式のvは一定ということになります。すると、fとλはお互いに補完しあう関係になります。つまりfの値が2倍の大きさになればλの値は2分の1になり、λの値が2倍になればfの値は2分の1になるのです。
角周波数(angular frequency)
ここでもう一つ重要な量をご紹介しておきます。角周波数、あるいは角振動数と呼ばれる量です。これは1秒間に円周上の点がどれくらいの角度進んだかを表す量です。記号はωで、単位はラジアンです。
$$ω=2πf$$
1ラジアンは半径rの円の円周上を長さrの分だけ進む角度なので、円周の長さが$2πr$で表されることを思い出せば、円の1周は$2πr/r=2π$ラジアンということになります。つまり360度=$2π$ラジアンです。
波動関数(wave function)
波に乗っている粒子の動きを数学的に記述することを考えます。弦の振動のような横波に乗っていることをイメージしてみると、粒子の点は下の図のように上下の運動を繰り返します。
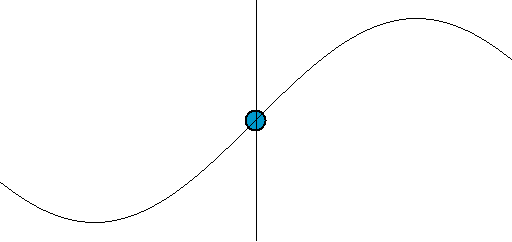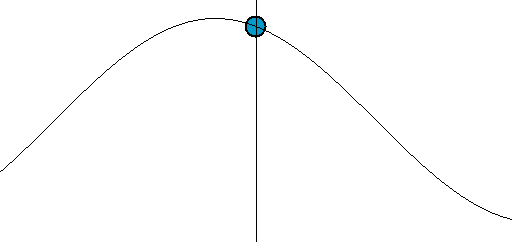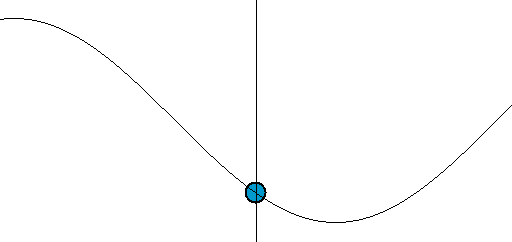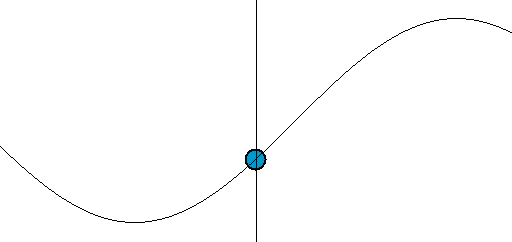
時間の経過に伴う動き
この粒子の上下運動を時間の経過と共に記述しようとすると、以下のようなグラフで表すことができます。縦方向のy軸が点の上下の移動距離を表し、横方向のt軸が時間の経過を表します。
水平方向のある点における動き
この粒子の運動はまた別の記述をすることも出来ます。ある時間tに時計を止めて、その瞬間を切り取った波の動きは以下のグラフで表すことができます。縦方向のy軸は上下の移動距離を表し、横方向のx軸は波の伝播の位置を表します。点が波のx軸上のどの位置にあるかによって、ある時間におけるy軸上の位置は異なります。よってyとtの他に、xというパラメーターが必要なのです。
波動関数
波動関数(Wave Function)は、波に乗っている粒子の位置を表す関数として捉えることとわかりやすいと思います。例えば、x=0つまり上記のxyグラフの一番左の場所における粒子の動きについて考えてみましょう。時間の経過に伴うこの粒子の動きは上のxyグラフのようになります。最大の振幅はA、1秒あたりに進む角度つまり角振動数はωだったので、時間に伴う波の動きは以下の式で表すことができます。
$$y(x=0, t)=A\cosωt=A\cos2πft$$
波がx=0からある位置xまで移動するのにかかる時間は、波の速度をvとするとx/vです。よって、時間tにおける、位置xでの波の状態は、時間t-x/vにおける、位置x=0における波の状態と同じです。つまり、波の上の一点のy軸方向の動きは、上記の式のtにt-x/vを代入して、以下の式で表すことが出来ます。
$$y(x,t)=A\cos[ω(t-x/v)]$$
ここで、 $\cos-θ=\cosθ$なので、この式は以下のように表すことができます。
$$y(x,t)=A\cos[ω(x/v-t)]=A\cos[2πf(x/v-t)]$$
つまりyは、時間tと位置x、両方の関数ということになります。さらに、$T=1/f$、$λ=f/v$より、
$$y(x,t)=A\cos[2π(x/λ-t/T)]$$
となります。あるいは、$T=1/f$より以下のように書くこともできます。
$$y(x,t)=A\cos[2π(x/λ-ft)]$$
波数(wavenumber)
さらに、波数と呼ばれる数kを
$$k=2π/λ$$
のように定義すると、$λ=2π/k$、$ω=2πf$を使って$v=λf$は、
$$ω=vk=2πf$$
とすることができます。よって上記の関数yは、
$$y(x,t)=A\cos(kx-ωt)$$
と書き換えることができます。
波動方程式(wave equation)
波に乗っている粒子の速度
この関数を使って、波に乗っている粒子の速度を求めることができます。これは波自体が進んでいく速度vとは異なり、y軸、つまり波の進行とは垂直方向の速度ということになります。y(x,t)はy軸方向の位置を求める式だったので、これを微分すればy軸方向の速度を求めることができます。波の速度$v$と区別するために、$v_y$として表します。
$$v_y(x,t)=\frac{\partial y(x,t)}{\partial t}=ωA\sin(kx-ωt)$$
偏微分(partial derivative)
ここで使われている$\partial$の記号は偏微分を表すものです。yはxとt両方の関数であるため、微分をするというとき、xについて、あるいはtについて微分することが可能です。ここでは速度を求めるので、xは一定として考え、時間tについて微分しています。よって偏微分が使われているのです。
波に乗っている粒子の加速度
今度は、波に乗っている粒子の加速度を求めます。加速度はyの二階微分で求めることができるので、以下のように表す事ができます。
$$a_y(x,t)=\frac{\partial^2 y(x,t)}{\partial t^2}=-ω^2A\cos(kx-ωt)$$
$y(x,t)=A\cos[2π(x/λ-t/T)]$なので、
$$a_y(x,t)=-ω^2y(x,t)$$
と書き換えることが出来ます。
xについての偏微分
上記では時間tについての偏微分を考えましたが、同様にxについて偏微分を取ることも可能です。xについて一階偏微分するとある点xにおける波の傾斜がわかり、二階偏微分するとある点xにおける曲率を出すことができます。
$$\frac{\partial^2 y(x,t)}{\partial x^2}=-k^2A\cos(kx-ωt)$$
こちらも$y(x,t)=A\cos[2π(x/λ-t/T)]$なので、
$$\frac{\partial^2 y(x,t)}{\partial x^2}=-k^2y(x,t)$$
となります。
波動方程式(wave equation)
tとxそれぞれについての二階偏微分には、$ω=vk$より、次のような関係が成り立ちます。
$$\frac{\partial^2 y(x,t)/\partial t^2}{\partial^2 y(x,t)/\partial x^2}=\frac{ω^2}{k^2}=v^2$$
これを書き換えた以下の式を、波動方程式(wave equation)と呼びます。
$$\frac{\partial^2 y(x,t)}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 y(x,t)}{\partial t^2}$$
まとめ
いかがでしたでしょうか?波を表すために導入された1つ1つの量とその関係がうまくイメージができれば、文系の数学の知識で十分理解できますよね。ここからもう一歩進めるとシュレディンガー方程式を理解することができます。ぜひシュレディンガー方程式をわかりやすく説明した記事も合わせてご覧くださいね。








